Introduction
Those of you with a sweet tooth are no doubt already familiar with the delicious doughnut, but did you know there is much more to that simple pastry than meets the eye? Here’s an experiment: take a sheet of A4 paper and roll it up, now try to join the two open ends without bending or making any corners on the paper, go on I’ll wait…..impossible right? Well that’s because we are stuck with only three dimensions, add in one more dimension though and you can! What’s more is that if we lived on the surface of that doughnut, the world would look a lot like the surface of the Earth does to us now-flat as far as the eye can see (but a lot sweeter if you choose to eat the soil). My research is on understanding all these ‘flat’ doughnuts (called tori in mathematics) and how to make new doughnuts from old ones by ‘melting’ them into new forms (because you can never have enough doughnuts!). Just to give you a taste of the full thing (!), it turns out that doughnuts really are all about the shape of the icing you use.
So today I'm going to give you three recipes to make some 0-calorie, four-dimensional doughnuts and for those culinary theorists out there, I'll also give a little insight to the magic behind these recipes.
Half-Ring doughnuts.
Ingredients:
- Icing (of your favourite flavour)
- Icing tube
- Rolling Pin
- A bowl
- 4-dimensional dough (available at all good mathematical bakeries)
- An oven
- Optional: A physicist, ability to move between three and four dimensions, patience
Step 1:Taking your bowl and icing tube, in a continuous fashion, draw a pattern of icing all the way around the bowl, coming back to where you started.
Step 2:Take your four-dimensional dough and flatten it using your rolling pin. Then roll it up into a sausage like shape.
Step 3:Place the sausage-dough along the bowl so that it matches up with the icing design from step 1.
Step 4:Bake until your pastry is golden brown and exists in a higher dimension. (At this stage you can ask for the help of an adult physicist to make sure you haven't broken any rules of the universe, after all no one wants to infamous for accidentally making a naked singularity! The shame would be unbearable).
Congratulations you've just cooked a (flat) four dimensional doughnut!
The Theory
Like any good chef I haven't revealed all of my secrets in the recipe, but you look like a trustworthy sort of person and seeing as it's just the two of us let me explain exactly what is going on here. Some good questions to ask here are "What exactly is going on here?", "What is 4-dimensional dough?" and "How does the baking actually work?" allow me to explain.
What is 4-dimensional dough? /How does the baking work?
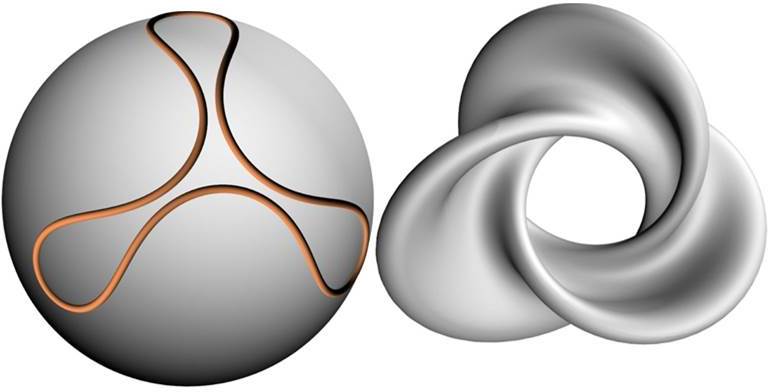
The idea behind the baking is essentially the following: imagine that you have drawn out your design using the icing, then to each part of the icing I attach a circle, if for example the shape I drew were a circle then what I end up with is a normal everyday ring doughnut. However, I'm not making just any old doughnut, mine is in four dimensions (so that my doughnuts can be flat and I can eventually retire to live on them without falling off the surface!) and so what I want to do is adapt this idea from three dimensions to four. The way to do this is to simply go from attaching 3-dimensional circles to the icing, to attaching 4-dimensional circles instead. What's a 4-dimensional circle I hear you ask! Well imagine I had a hula hoop, which will do as a stand in for our 3-dimesional circle. Then I can describe it by telling you how wide it is and how high off the ground I am holding it, a 4-dimensional circle is almost exactly the same except it has another measurement in addition to width and height. So really the 4-dimensional dough and baking is just the attaching of these circles to the icing which is why I call them half-ring doughnuts (mathematically they are called Hopf tori after the mathematician Heinz Hopf who discovered this method of attaching circles in 4-dimensions).
Flat doughnuts
Ingredients:Same as the ingredients for half-ring doughnuts.
Step 1:Make two half-ring doughnuts using the previous recipe.
Step 2: From each of the half-ring doughnuts cut out the dough with icing on it.
Step 3:Using some icing join the two pieces of dough together at a single point.
Step 4:Bake.
Congratulations, you now have a (no-ring) flat doughnut!
The Theory
Here we start with two half-ring doughnuts and extract the bits with icing, the design of the icing may have changed slightly with the move of it from 3-dimensions to 4-dimensions. It will turn out that the doughnut that we end up with will again be flat, but of course since I'm not attaching any circles anywhere unlike in the first recipe, the doughnut I end up with will be totally different to any I've made before. In fact all flat doughnuts are made in this way with them being flat coming about as a result of the two half-ring doughnuts being flat.
My Research: Finite Type Flat doughnuts, doughnuts for the lazy.
The previous recipe is a bit hard, it requires us to be able to work in 4-dimensions and the icing patterns can be very, very complicated, so for those of you dimensionally-challenged, I present my own special recipe for making a special type of doughnuts which also double as a recipe for people like me who are lazy and can't be bothered with intricate designs (and for those who forget to set the oven timer when baking!)
To eliminate the really complicated designs and to not have to worry about how long we bake, let's only use icing designs that
- Don't drip off the bowl when heated.
- Eventually stop melting when heated.
If we only use these designs, then what we get are icing patterns that always stay on the bowl no matter how long we forget them in the oven and who, if we leave them baking for long enough will not keep changing.
If we only use these designs and bake in the usual way then what we get is some flat doughnuts that stay flat doughnuts no matter how long we bake them. In fact over baking them allows us to melt the icing and make different types of flat doughnuts just by over baking and not by having to make different icing designs from the start. Hooray for being lazy!
The Theory
So why did I include the rather ominous looking title 'finite type' in the heading, what does this term mean? Well, imagine I have a piece of string placed in a circle around a globe. Then using my thumb I can add a little bump to this shape so that it is no longer a circle and I can do this several times. This is essentially what happens when I 'melt' the icing, so what I would like from this recipe is to only use designs that stay on the bowl ( I need this to be able to use my previous two recipes) and more importantly eventually stop melting so that I know when the baking is finally complete. Mathematically these sort of designs are known as finite type (i.e. they only melt a finite number of times before stopping) and what makes this recipe so special is that given any flat doughnut from recipe one or two, I can produce a finite type flat doughnut that is very, very (in fact as many verys as you want) close to the shape of the doughnut you have given me without having to resort to complicated designs or existing in four dimensions. In fact the motivation behind my research is precisely this, while we know a lot about the half-ring doughnuts and know that flat doughnuts that do not involve the use of a circle exist, they are not very well studied. My research allows us to start with something we know (the half-ring doughnut) and melt it into a flat doughnut about which we know very little and by studying what the melting does we can then say something about the flat doughnut that we end up with. In particular these objects are important as physicists are almost certain (within 0.4% of being absolutely certain) that the universe is flat and so in studying these flat tori we can attempt to understand a potential model for the shape of the universe.