If the price of avoiding non-locality is to make an intuitive explanation impossible, one has to ask whether the cost is too great. (David Bohm)
Introduction
Quantum mechanics is the physics of the very small and the very cold. When particles are small and cold they take on wave properties and thus act differently to anything you can imagine in the world you see around you. Throwing tennis balls through brick walls, walking through two adjacent doors at the same time, even having a cat that is both dead and alive at the same time might seem weird to you, but in quantum mechanics this is quite normal. It is this strange playground of physics that has attracted people to quantum mechanics, and the advent of cold atom technologies allows us to, not only theoretically but physically, study these weird systems. In recent years, cold atoms have provided an excellent testbed for investigating these quantum effects. As the system is cold, it is incredibly clean and noise-free due to the lack of thermal vibrations and collisions with particles around it.
Quantum Entanglement
One of the most bizarre concepts of quantum mechanics is quantum entanglement. Entanglement was very controversial when it was discovered during the formulation of quantum mechanics and even today it still amazes and astounds physicists. At its heart it is quite simple; if we have two particles and they are entangled, we cannot know everything about one particle without knowing everything about its entangled partner. At first this may seem trivial, but in fact it is very powerful. For example, say I have two dice and I put them into a machine that creates entanglement. I then give one die each to two different people and I send them into two different rooms so that they cannot communicate with each other. I ask them to roll their dice and record the outcome of the dice roll. At the end of the exercise I take the two lists of the dice outcomes and I compare them. I find something astounding has happened, the two lists are exactly the same, if one person rolls a six then the other person rolls a six, if one person rolls a two then the other person rolls a two, etc. This is strange as the outcome from rolling a dice is entirely random, yet each random throw of the dice results in the same number on both dice. As a result of the entanglement between the dice there are correlations in the "measurements" performed on each dice. What is even stranger is that the distance between the dice does not matter; if one person was sitting in Cork with one of the entangled dice, and the other person was in a rocket going to Neptune, they would still roll the same outcome every time. Due to the entanglement, there is a connection between two particles no matter where these particles are and we can use this property in upcoming future technologies.
The potential of entanglement stretches far beyond playing dice. Current research in the area of quantum technologies revolves around exploiting quantum entanglement to ensure 100% secure communications. With classical communications a message is sent and is encoded with a random encryption key which both parties hold, and the resulting message is decoded using this key. However an eavesdropper can intercept and also receive this key and can attempt to break the code, hence uncovering the secret communication. However, by exploiting the strange effects of entanglement we can ensure secure communications. If Alice creates these entangled particles and keeps one half of the set and sends the other to Bob they can use these particles to send a private message. If an eavesdropper Eve intercepts Bob's entangled particle, and tries to send a duplicate atom to Bob, both Alice and Bob will be able to detect that someone is listening as the entanglement between Alice's particle and Bob's stolen particle will be broken. The transmission of the message is then stopped and no information has been stolen.
My Research
My research involves theoretically investigating whether entanglement is present between two atoms held by a harmonic trapping potential. A harmonic trap is a mathematical model that is a very good approximation of most traps made in experimental labs. The harmonic potential is a beautiful model in physics due to its simple solution and evenly spaced energy spectrum. The model I investigate has two atoms in separate harmonic traps. I can manipulate the system by changing the distance between these particles or tuning the interaction between these particles. By changing these parameters I can see how the entanglement would be affected if the particles are on top of each other or far away from each other, if they can interact or if they can't. What is particularly nice about this model is the fact that, unlike many problems in physics, it is mathematically solvable. This ensures that numerical techniques are not needed to solve the equation, eliminating the associated risk of introducing errors into the calculation.
To calculate the entanglement in this system I use a measurement, first formulated by Northern Irish physicist John Bell in 1964, that measures the non-locality between two particles. Non-locality is the direct influence of one object on another distant object, which is what happens between our entangled particles. So in this case non-locality implies entanglement. John Bell formulated an inequality which when calculated to be less than 2 means that there is no non-local correlations between the particles and thus no entanglement. However if this measurement is greater than 2 there is non-locality and entanglement present between the particles. This is a very powerful experimental tool that was first used in 1982 and has been a staple of quantum information experiments ever since.
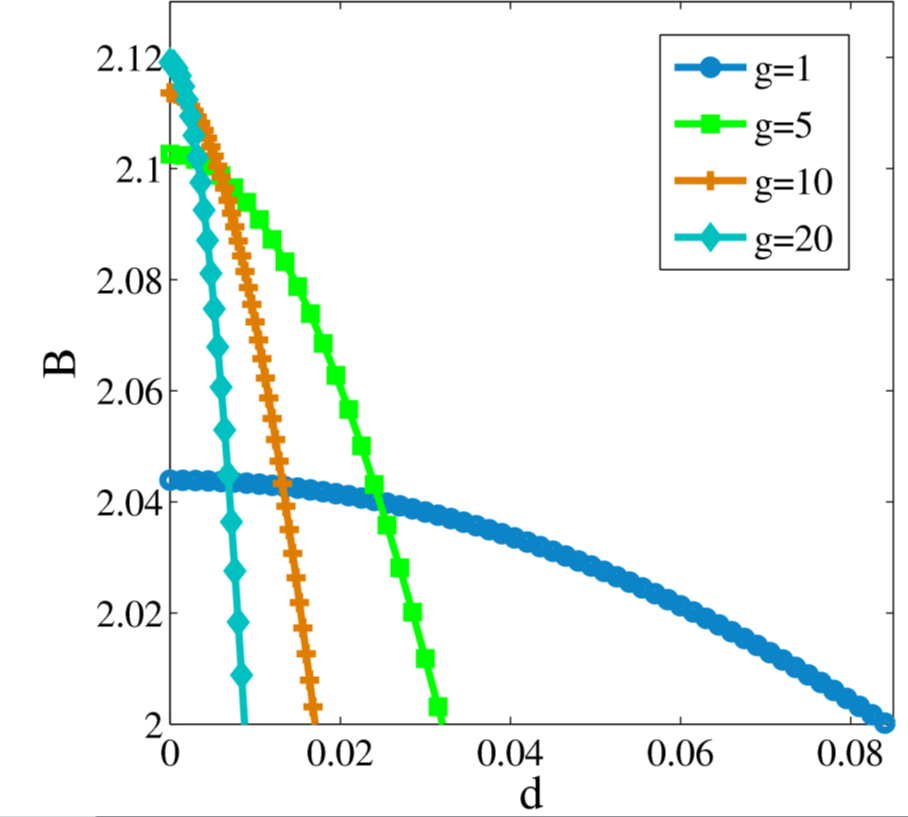
Violation of Bell's inequality is evidence for non-locality between the two particles, and hence these particles are entangled.
Here the violation is plotted against interparticle distance for different values of the particle interaction, g. Intuitively
if g is large the particles interact more and the entanglement should be large. Interestingly it is seen from the figure that
entanglement lasts longer for lower interaction strengths, but it is not as strong as the large interaction case when the
particles are in direct contact with no separation.
For my model there was entanglement calculated between the two particles. In Fig.1 I have plotted the violation of the inequality versus the distance between the particles. As can be seen the entanglement dies off when the particles are at large distances from each other. This makes sense as we cannot entangle two particles at different sides of the earth if they have never been in contact with each other. From this data we know that the particles must be very close to each other to create entanglement between them, but once this entanglement is created, we can separate them out and the entanglement will survive. Another thing apparent from the data is how the entanglement changes with the interaction between the particles. With increasing interaction we get an increasing entanglement; however for a low interaction we see that the range of the entanglement is greater than that for a high interaction. Classically speaking this is counter-intuitive, how can a smaller interaction be more resilient to the changing distance between the particles? For the answer we need to delve into the dynamics of our particles. The interaction is inversely proportional to the scattering length of the particle, so if we increase the interaction, we decrease the scattering length. The scattering length is the range of the interaction, so the larger the scattering length the greater distances the particles can interact over.
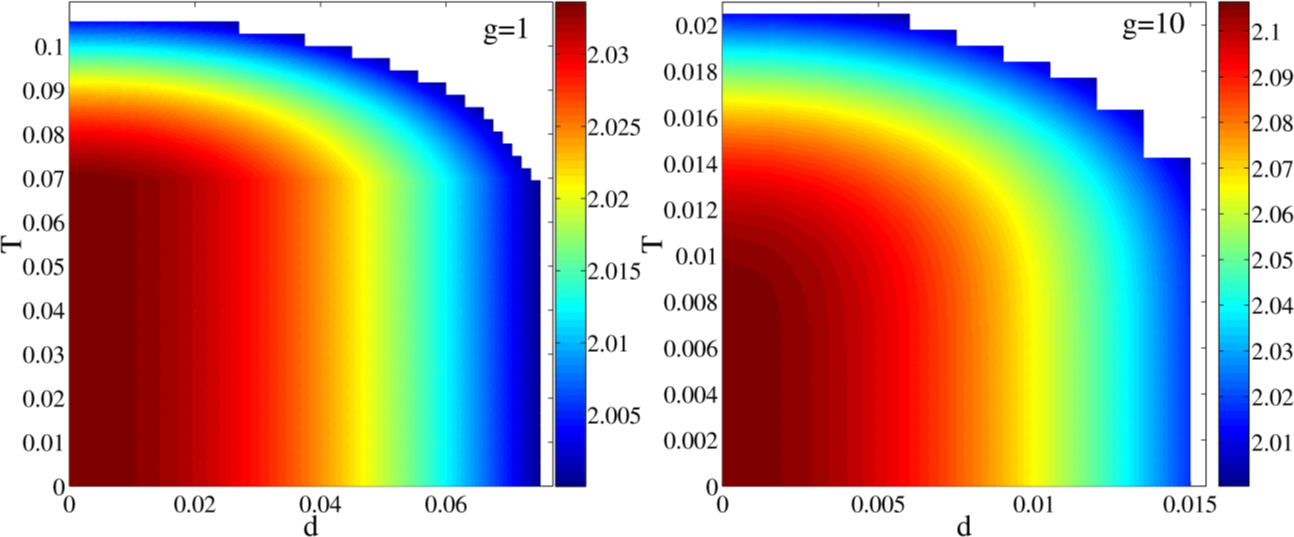
In the left panel the interaction is low, g=1; in the right panel the interaction is high, g=10. The intensity of the violation
is graduated in the colour scale from blue to red. It is plotted against temperature and particle separation , both of which
are scaled. It is evident from the graphs that the lower interaction is more resilient to higher temperatures than the larger
interaction strength.
We have seen that low interactions are more resilient to changes at zero temperature, or zero degrees Kelvin, but what happens when we introduce temperature as a variable in our system? This is a practical concern as physically we can never reach zero Kelvin, but we can get very close to it. Fig.2 shows the variation of entanglement with applied temperature for particles with a low interaction and a high interaction. Again we see that the entanglement is more resilient to temperature change for low interactions and more sensitive for high interactions. High temperatures destroy the entanglement as our state is no longer in the clean, pure regime but is in a mixture of higher order modes. Very low temperatures are essential for the generation and control of entanglement, this means experiments must be carried out near zero degrees kelvin also known as absolute zero which is -273.15°C, at these temperatures it would be the coldest substance in the known universe, even colder than the vacuum of space. This system can be experimentally created in laboratories and can be used as good testbed to detect entanglement between ultracold atoms. We are at exciting time in science where we can create these experiments that are so accurate and clean that the fundamentals of physics can be rigourisly studied and to be able to understand something as strange as entanglement will be an amazing achievement.
Outlook
Future work will concentrate on investigating entanglement between more particles, and looking at the strange effects that can found in one-dimensional cold gases. One such example is a NOON state in which particles on a ring rotate clockwise and counterclockwise at the same time. This is analagous to Schrödinger's famous, if unfortunate, cat which was both dead and alive at the same time. Another interesting idea is the Anderson orthogonality catastrophe which tells us that if a system is suddenly perurbed there is zero probability that our system will act in the way that we expect. So, for example, if we suddenly give a gas a “kick” surprisingly nothing happens......
Thomás Fogarty is a student in the Ultracold Quantum Gases Group under the supervision of Thomas Busch. The author would like to acknowledge IRCSET for funding my research under the EMBARK initiative RS/2009/1082.

