Introduction

Thin-walled structures, also known as shells, combine light weight with high strength and are used in a diverse range of fields including aerospace engineering, civil engineering and chemical engineering. Common applications of these shells include oil and gas storage tanks, powder or liquid storage tanks in pharmaceutical plants as well as airplane frames and ship bodies. Although these thin-walled shells have a wide variety of uses, this research is motivated by storage tank collapse in the process industry. Thin-walled cylindrical tanks common in the food and biotechnology sectors are prone to buckling (or inward collapse) due to accidentally induced internal vacuum. During the sterilisation process, steam can condense, causing a reduction in volume. This results in an equivalent increase in external pressure, triggering collapse, or buckling of the tank. Such a collapse, if it occurs, tends to be catastrophic resulting in the complete destruction of the vessel (see Fig.1). Notwithstanding that the basis of this type of failure is understood and can generally be averted, it is still a regular occurrence, often due to the inadvertent closure of line control valves during a sterilisation cycle.

Large discrepancies exist between classical shell buckling theory and results of shell buckling experiments. Experimental values have been shown to fall anywhere between 20-70% of the theoretical value. This wide disparity has been attributed to two main factors, namely:

• Geometric imperfections
• Material variation

Geometric imperfections comprise any geometric feature which distinguishes the tank from a perfect tank. In an ideal world, the perfect tank would be perfectly circular and have a smooth uniform wall surface. However, many imperfections may be caused during the manufacturing process of the tank including dents, welded seams, wall thickness variation, out-of-roundness or non-circularity. These imperfections all affect the performance of the shell.

Material variation accounts for a non-uniformity of the material used, such as variation of strength in the metal. The aim of this research is to find the factors influencing this type of collapse and find an improved method to predict and prevent collapse.

Methods of Research

This research is divided into two major categories: experimental and numerical.

Experimental

Experiments are carried out in the laboratory on small-scale steel cans in order to replicate the behaviour of the real tanks. The manufacturing process of the cans is as follows:

• The main body of the can is cut from a flat sheet of rolled steel
• The main body of the can is passed through rollers which bend it into a circular shape so that the two ends meet
• The meeting ends are welded together forming a seam
• The top and bottom of the can are added on by means of a folding process

These cans contain imperfections typical of those caused inadvertently by the manufacturing process and so are suitable for this study.

The cans are positioned on an experimental rig with openings at each end. Steam at 100°C flows in one end, pushing out cooler air through an outlet pipe at the other end. At each end is a valve and when the can has been filled with steam and the cooler air emptied, the valves are closed, sealing the can so no steam can escape. The cans are allowed to cool under normal atmospheric conditions in the laboratory. As the steam cools it contracts creating a vacuum, or increase in external pressure. This leads to an instantaneous sucking-in of the can walls, the buckling, and ultimate collapse of the can (See Fig. 2). Throughout the experiment, pressure inside the can is monitored in order to record the buckling or collapse pressure at the point of collapse of the can. By carrying out experiments on a large number of cans, we can quantify the dispersion of the collapse pressure.

The deformed shape of the can is unusual. The can deforms with six panels (or lobes) forming a hexagonal cross-section. This deformed shape is geometry dependent and so for a longer can, or one with a greater wall thickness, the deformed shape might have maybe 8 panels or 20 panels.

Imperfection Measurements

Since geometric variability is known to be a major factor influencing this collapse, geometric surveys of the cans were conducted. A measurement rig was custom-built to take full surface geometric data of the cans allowing us to record any imperfection. The cans were centred and secured on a base plate which rotated 360°, and four dial gauges, recording surface data, moved vertically on linear actuators. Three of the dial gauges were positioned at 120° intervals outside the can with the fourth on the interior, recording thickness imperfections. The base plate rotates and the actuators move vertically until measurements of the entire surface of the can are taken.

Finite Element Analysis

This real-can geometry is then modelled and analysed using finite element analysis software. In this way, all geometric imperfections of the cans may be modelled. This allows us to predict more accurately the behaviour of the cans. Finite Element (FE) Analysis is the state-of-the-art in engineering analysis and is used in all modern structural analysis and design. A model of the structure is created in the software program which then performs an analysis using preset loading and boundary conditions. The loading conditions describe how much force or pressure the structure is subject to while the boundary conditions describe the fixity of the structure, i.e. how free it is to move. The model was set up as shown in Fig. 4 using the same geometry and material properties as the experimental cans.

The analysis is then performed (See Fig. 5) and results are compared to the experimental behaviour.

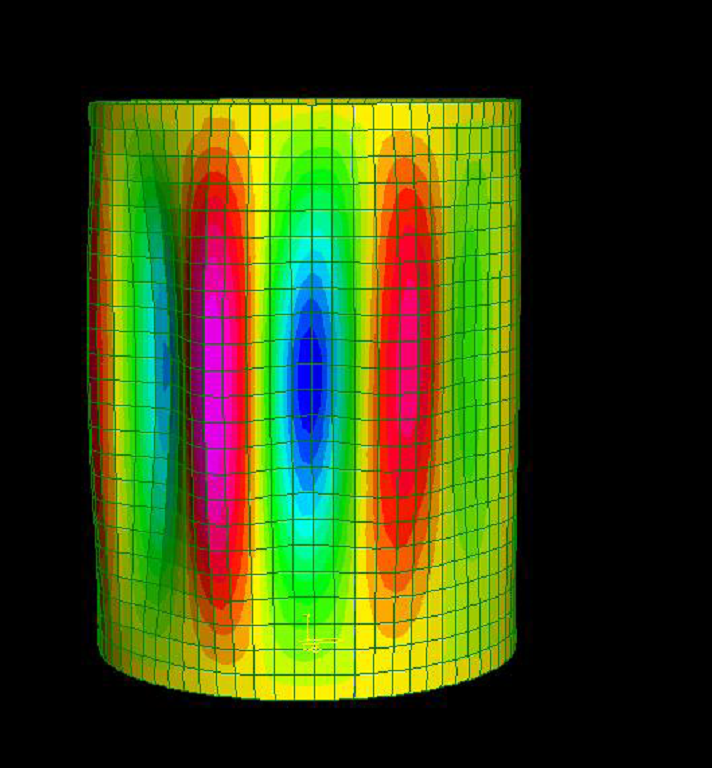
Results and Discussion

The buckling pressures predicted by the Finite Element Analysis are in good agreement with the experimental collapse pressures (see Table 1). Three of the cans are within 7% and the other two are within 12%. The reason for this larger discrepancy is that there was a problem with the steam inlet pipe during the experiments for cans A and D and so this affected the data somewhat. The FE analysis tends to overestimate the buckling pressures slightly and also over predicts the number of lobes. This may be possibly due to other unobserved geometric imperfections in the real cans that aren’t included in the numerical analysis.

Conclusion

An experimental and numerical analysis of the buckling of cylindrical shells under a uniform external loading is presented. Geometric imperfections based on measured data of five cans were modelled in a nonlinear finite element analysis. Buckling collapse experiments were carried out in the laboratory and the results compared. The study shows that the numerical analysis of the buckling process predicted by the FE model closely follows the experimental behaviour.

Caitriona de Paor is a student in the Department of Civil and Environmental Engineering under the supervision of Dr. Denis Kelliher and Dr. Kevin Cronin. The author would like to acknowledge contributions to this research from Dr. William Wright, Sean McSweeney, Paul Conway, Tim Power and Michael O’Shea and funding from IRCSET Embark Initiative.